Optimized Counting of Common Neighbors/Vertices in GSQL
- Blog >
- Optimized Counting of Common Neighbors/Vertices in GSQL
By Prateek Agrawal
Graph analytics plays a crucial role in finding hidden relationships within large datasets. One fundamental operation in this domain is calculating the number of common neighbors between pairs of vertices in a graph. This has applications in similarity measurement, link prediction, graph compression, community detection, and more.
Current multi-threaded approaches often rely on set intersection techniques or do not easily lend themselves to parallelization. In this blog post, we’ll explore:
- An optimized algorithm for counting common neighbors that outperforms the set intersection method.
- How to implement this optimized algorithm in GSQL, a Turing-complete language.
- A comparative performance analysis of both methods.
1.0 Counting Common Neighbors/Vertices
In a graph, vertices (also known as nodes) represent entities, and edges signify relationships between those entities. If an edge connects two vertices, we say those vertices are neighbors. If vertex C is a neighbor of vertex A, and C is also a neighbor of vertex B, we say that C is a common neighbor of A and B.
Some use cases that can utilize the common neighbors are described below:
- Community Detection: Identifying vertices that have a high number of common neighbors can indicate that they belong to the same community or cluster within the graph.
- Recommendation Systems: Common neighbors can be used to make recommendations. If two users in a social network have common friends, it might suggest they have shared interests.
- Link Prediction: Analyzing common neighbors can help predict potential connections between vertices that are not directly linked yet. If two vertices share many common neighbors, there’s a higher chance they might form a direct connection in the future.
- Graph Similarity: Comparing the sets of common neighbors between vertices can be used to measure the similarity or relatedness of vertices within the graph.

1.1 Merchant-Merchant Graph Use Case
In the use case below, we will be using a graph that captures how strongly two Merchants, represented by point-of-sale (POS) devices, are connected to each other based on common distinct credit or debit Cards that are used at both Merchants. See Figure 1 below.
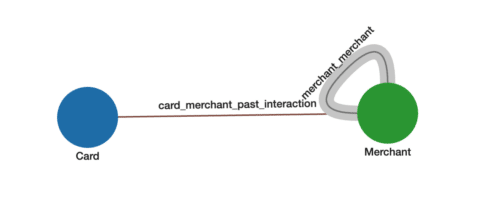 Figure 1. Merchant-to-merchant graph schema.
Figure 1. Merchant-to-merchant graph schema.
For the Merchant-Merchant Graph:
- Each Merchant vertex and Card vertex represents a distinct entity
- The edges card_merchant_past_interaction come directly from Card (shopper) to Merchant transactions.
- The weighted edges merchant_merchant between two Merchants represents how many common Cards are shopping between the two Merchants. These edges and their weights are not in the original data but are the result of analyzing the graph. The higher number of common Cards between two Merchants, the higher the weight and stronger the connection.
If a shopper is shopping at a given Merchant, we can use the strengths of connections to predict which other merchants they are most likely to shop at (recommendation). Or this metric can also be used as a signal for fraudulent transactions (fraud detection).
The schema for our graph looks like below where card_merchant_past_interaction edges are already available to us and we want to insert merchant_merchant edges and their corresponding weight.
Figure 2 shows an example of how merchant_merchant weighted edges would be inserted. The edge weight inserted between the two Merchants is 4 because 4 cards are in common between the two Merchants:
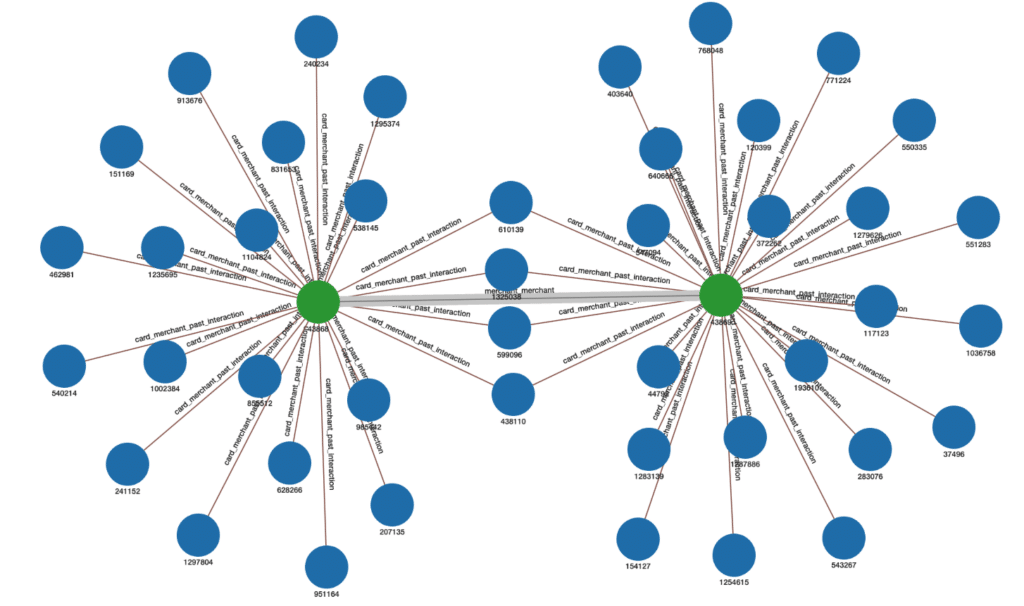
Figure 2. Example of weighted edge representing the number of common Cards between two Merchants.
2.0 Complexity Analysis and Optimization
2.1 Time Complexity of the Naive Intersection Method
To count the common neighbors (Cards in this case) between two given (Merchant) vertices A and B, we can collect the set of Card neighbors of A, those of B, and do a set intersection between the two. The time complexity for this algorithm can be determined as follows:
- Getting Neighbors for Vertex A and B: Retrieving the set of neighbors for a single vertex in an adjacency list representation of an undirected graph takes O(K) time, where K is the degree (number of incident edges) of the vertex. So, for vertices A and B it would take O(K_a + K_b) time to collect the sets of neighbors.
- Calculating Intersection: Finding the intersection of two sets with sizes n and m would generally require O(n+m) time. In our case, n=K_a and m=K_b, the number of neighbors for vertices A and B, respectively.
Time complexity for a single pair:
Combining these steps, the time complexity to calculate the Common Neighbors for a single pair of vertices (A,B) would be O(K_a + K_b).
Time complexity for all pairs:
For calculating Common Neighbors for all possible pairs of n vertices in the graph, we would need to perform this calculation n(n-1)/2 times, leading to a worst-case time complexity of O(n2K), where K is the maximum degree in the graph.
It is possible to not count intersections for all n2 pairs. To be a common neighbor, a (Card) vertex must have at least two neighbors. For each card, we can collect its list of neighboring Merchants and only continue to work with those having degree K ≥ 2. This takes O(nK) time. We only need to calculate the intersection between Merchants on these neighbor lists. The worst case length of this list would be degree K. Hence the new worst case time complexity for n vertices becomes O(nK2).
2.2 Optimized Time complexity
The optimized method aims to reduce the time complexity by altering the approach to how we count the common neighbors (or “Cards”) between two vertices (or “Merchants”) A and B. Instead of creating sets of neighbors for two merchants A and B and then finding their intersection, this method uses a direct counting approach.
Consider the Example of three Cards (C1,C2,C3) and five Merchants (M1,M2,M3,M4,M5) connected as in Figure 3:
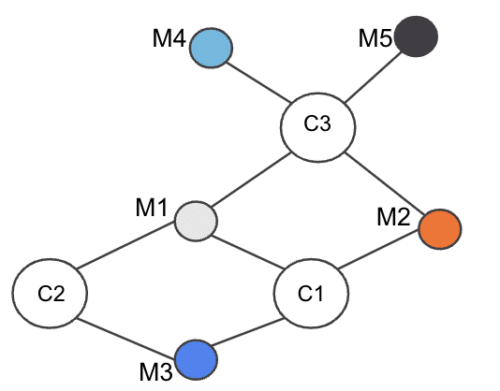
Figure 3. Merchant-Card graph example
Our objective is to find the number of common cards between each Merchant-Merchant pair.
Consider Merchant pair (M1,M3). To compute the common Cards between M1 and M3, find the set of Cards neighboring M1, i.e., S1 = {C1,C2,C3}. Next find the set of Cards neighboring M3: S2 = {C1,C2}. Now if we run the intersection , we see the set size is 2, i.e., 2 cards are common between M1 and M3. Running for all Merchant pairs M1 to M5, we can get the edge weight for all pairs of Merchants with O(nK2) complexity.
However, instead of doing intersection for each merchant pair, we can compute the edge weight using the following steps:
- Find the set of all Merchants shopped at by a Card (neighbors of the Card)
- For each Card, get each pair of Merchants in the set and do:
- Add a merchant_merchant edge if it doesn’t exist, with initial weight of 0
- Increment edge weight by 1
So for our example above in Step 1, we find all neighbors of each Card:
- C1 Set: (M1,M2,M3)
- C2 Set: (M1,M3)
- C3 Set: (M1,M2,M4,M5)
And then we iterate over each card and each Merchant pair in the set, incrementing the edge weight by 1:
- For C1 edge weight update applied:
- (M1,M2) += 1 → 1
- (M2,M3) += 1 → 1
- (M1,M3) += 1 → 1
- For C2 edge weight update applied:
- (M1,M3) += 1 → 2
- For C3 edge weights update applied:
- (M1,M2) += 1 → 2
- (M1,M4) += 1 → 1
- (M1,M5) += 1 → 1
- (M2,M4) += 1 → 1
- (M2,M5) += 1 → 1
- (M4,M5) += 1 → 1
Hence the final edge_weight pairs are as shown in Figure 4:
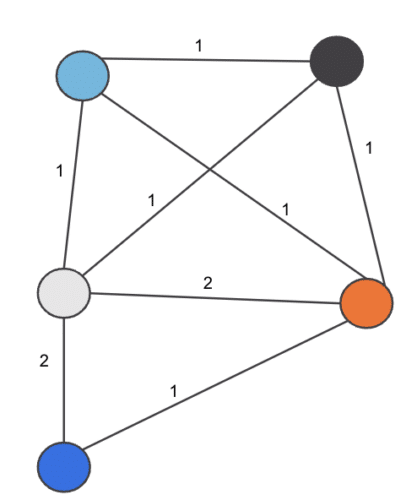 \
\
Figure 4. Weighted edges between Merchants
Hence we see from the example the time complexity can be optimized by observing the fact that we can count the number of common vertices between two vertices instead of doing an intersection and the counting operation can be done in O(1) and hence the complexity can be reduced from O(n K2) to O(nK).
3.0 Implementation in TigerGraph Using GSQL
To execute Common Neighbors algorithms, we will utilize the TigerGraph database as our graph data storage and use GSQL for algorithm implementation. Because of TigerGraph’s distributed nature we can run the algorithm distributedly and with memory efficiency.
We will evaluate performance differences between the intersect method and the optimized approach by using the above pre-established use-case: calculating common cardholders who shop at two different merchants and then assigning a weighted edge between those merchants based on that count.
The files for building Schema/Load Data and running queries in TigerGraph are in the appendix.
3.1 Intersect method GSQL implementation:
The query below shows the implementation of the Intersection method and how to insert the merchant-merchant edges in O(nK2) time.
CREATE DISTRIBUTED QUERY _02_common_cards_intersect(
INT min_edge_weight = 1
)
FOR GRAPH optimizing_common_neighbors {
SetAccum @merchants;
MapAccum<VERTEX, INT> @edge_weight;
DATETIME before;
cards = {Card.*};
before=(now());
// Collect all Merchants on the Card
merchants = SELECT m FROM cards:c- (card_merchant_past_interaction:e) - Merchant:m
ACCUM c.@merchants+=m; //O(M) where M= number of cards
PRINT "Time to collection of merchants on cards ",datetime_diff(now(), before);
// INSERT edges and weights using the INTERSECT method.
before=(now());
temp = SELECT m FROM merchants:m -(card_merchant_past_interaction:e)- Card:c
ACCUM
FOREACH merc IN c.@merchants DO // O(N*K) where N =number of Merchants and K= Max degree of Card
IF getvid(m) < getvid(merc) THEN
tg_common_neighbors(m,merc,min_edge_weight) //O(K_a+K_b) where K_a and K_b are the degrees of the merchant pair
END
END; //Total complexity O(N*K*(K_a+K_b))=O(N.K^2)
PRINT "Time to INSERT edges using intersect method",datetime_diff(now(), before);
}
The sub-query tg_common_neighbors called in the above query does the actual intersection in O(K_a + K_b) time.
Below is the sub query logic:
//Intersect subquery
CREATE QUERY tg_common_neighbors(
VERTEX v_source,
VERTEX v_target,
INT min_edge_weight
)
FOR GRAPH optimizing_common_neighbors {
avs = {v_source};
bvs = {v_target};
INT sz;
na = SELECT n
FROM avs -(card_merchant_past_interaction:e)- :n;
nb = SELECT n
FROM bvs -(card_merchant_past_interaction:e)- :n;
# Get neighbors in common for source and target and compute the common neighbors
u = na INTERSECT nb;
sz=u.size();
# Insert edge only if the weight is >= min_edge_weight
IF sz >= min_edge_weight THEN
INSERT INTO merchant_merchant (FROM ,TO ,weight) VALUES (v_source,v_target,sz) ;
END;
}
3.2 Optimized Common Neighbors implementation
For optimization we simply replace the intersect sub query tg_common_neighbors by counting the edge weight for each merchant-merchant vertex pair and hence reduce the complexity to O(K).
CREATE DISTRIBUTED QUERY _02_common_cards_optimized(
INT min_edge_weight = 1
)
FOR GRAPH optimizing_common_neighbors {
SetAccum @merchants;
MapAccum<VERTEX, INT> @edge_weight;
DATETIME before;
cards = {Card.*};
before=(now());
// Collect all Merchants on the Card
merchants = SELECT m FROM cards:c- (card_merchant_past_interaction:e) - Merchant:m
ACCUM c.@merchants+=m; //O(M) where M= number of cards
PRINT "Time to collection of merchants on cards ",datetime_diff(now(), before);
// Establish logical edges an summed weights
before=(now());
temp = SELECT m FROM merchants:m -(card_merchant_past_interaction:e)- Card:c
ACCUM
FOREACH merc IN c.@merchants DO // O(N*K) where N =number of Merchants and K= Max degree of Card
IF getvid(m) < getvid(merc) THEN m.@edge_weight += (merc -> 1) //O(1)
END
END; //Total complexity O(N*K*1)=O(N.K)
PRINT "Time to establish merchant-merchant edges using optimized common neighbors ",datetime_diff(now(), before);
// Insert edges
before=(now());
temp = SELECT m FROM merchants:m
POST-ACCUM
FOREACH (merc, w) IN m.@edge_weight DO
IF w >= min_edge_weight THEN // Insert edge only if the weight is >= min_edge_weight
INSERT INTO merchant_merchant VALUES (m, merc, w)
END
END;
PRINT "Time to INSERT merchant-merchant edges ",datetime_diff(now(), before);
}
4. Performance Comparison
For comparing the performance of the two algorithms the data metrics and hardware being used are as follows:
Data Metrics:
| Metric | Count |
| All Vertices | 1,807,672 |
| All Edges | 6,872,163 |
| Vertex “Card” | 1,335,486 |
| Vertex “Merchant” | 472,186 |
| Edge “card_merchant_past_interaction” | 6,872,163 |
| Edge “merchant_merchant” | 0 |
Raw Data size = 95.1MB.
The final count of “merchant_merchant” edges inserted is 20,607,316.
Hardware Configuration:
2 x TG.C16.M64 TigerGraph Cloud instances (16 CPUs, 64GB Memory)
The following Table captures the performance of the two algorithms.
| Metric | Intersection Method | Optimized Method | Notes |
| Execution Time (Seconds) | 3517.49 | 23.33 | 153x Speed improvement |
| Peak Memory Usage (GB) | 8.1 | 2.1 | 4x Memory reduction |
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
5.0 Conclusion
The optimized algorithm significantly outperforms the intersection-based approach, not just in speed but also in memory efficiency. TigerGraph’s GSQL enables users to tailor algorithms to their specific needs, offering unparalleled flexibility and scalability. For additional examples of graph algorithms implemented in GSQL, please refer to our Graph Data Science Library.
Appendix
Solution that can be run in GSQL shell Notebook to create Schema/Load_data/install queries Graph Data File for Card-Merchant Edges If you’re interested in exploring how TigerGraph can open up new dimensions with your data, you can sign up for a free instance of TigerGraph Cloud at tgcloud.io or contact us at info@localhost.